4.3 Images (class GipImage)

Image artifacts are represented by the GipImage class, which is like all distributed artifacts inherited from the Artifact class. The image data itself is stored as an instance of the AWT class java.awt.Image. A java.awt.Image object can encapsulate all types of images and provides useful methods to deal with images. The image itself is displayed by a frame defined by the ImageWindow class. An instace of the ImageWindow class is created and returned by the display method (see Chaper 4.1). The GipImage class provides also methods that are used to load, save and filter the image:

4.3.1 Loading Images

A newly instantiated GipImage is empty and does not contain an image. An image is loaded through the methods loadImage and loadImageFromURL. The first method loads an image from the clients file system. The second method loads an image from the World Wide Web designated with a URL. Both methods are able to load GIF and JPEG images. This is done with the getImage method of the AWT Toolkit class. The method loadImage also supports PNG images. PNG (portable network graphics) is a new upcoming image file format that is supposed to replace CompuServe's GIF, since the compression algorithm used in GIF is patented by Unisys Corporation and can not be used freely in commercial products [9]. Developing routines for loading and saving PNG files is a complex task. The freely available PNG package from VisualTek Solutions, Inc. has been used instead. PNG files are loaded by using the package's PNGDecoder class.

4.3.2 Saving Images

The image is saved to a file by calling saveImage of the GipImage object. This method allows saving the image in several file formats. The following table shows the supported formats and the software packages that have been used. Those software packages are freely available and can be used in non-profit applications.

Image Format	Software Package	Link to distributor
GIF	GifEncoder class by Jef Poskanzer <jef@acme.com>	http://www.acme.com/java/
JPEG	JpegEncoder class by James R. Weeks and BioElectroMech	http://www.obrador.com/
PNG	PNGEncoder class from the Java PNG Library by VisualTek Solutions Inc.	http://www.visualtek.com/PNG/
PPM	PpmEncoder class by Jef Poskanzer<jef@acme.com>	http://www.acme.com/java/

   
4.3.3 Manipulation of Images with Java Image Filters

Java's AWT defines two Java interfaces named ImageConsumer and ImageProducer, which must be used to deal with an AWT images raw image data. The ImageConsumer interface is responsible for retrieving data from an image and the ImageProducer interface is used to produce image data. The AWT supports a standardized way of image manipulation by providing the jave.awt.ImageFilter class. This class implements an ImageConsumer interface and is further placed between an image producer and image consumer. It takes image data from the image producer, manipulates (filters) that data and makes it accessible through it's ImageConsumer interface.

  

Figure 4.8: The chain of image consumer and producers.

At first, it seems complicated to access an image through a pair of ImageConsumer/Producers. However, it is a modular and uniform way to access and manipulate images. Many image filters can be placed in series that way and none of the filters has to worry about how the image has been created and how it is stored internally by its predecessor. Another advantage of this method is that image filters can be easily used in other applications without changing a single line of code. All image manipulation functions in this project, like geometrical transformations and mask filters, have been implemented in this fashion. The image contained in a GipImage object is filtered by calling its filter method. It takes an instance of the ImageFilter class and applies that filter to the image. The current image is replaced by the output of the image filter.

4.3.3.1 Writing an image filter

The actual task of writing an image filter is the implemention of its ImageConsumer interface. The image filter manipulates the image data before it is forwarded to the following image consumer. An instance of the raw AWT ImageFilter class can be considered a null Filter. It only creates an identical copy of the source image. A subclass of the ImageFilter class has to be created and two important methods have to be overridden in order to create a useful filter:

• setPixel: This is called by the image producer that delivers the image data for the image filter. A rectangular area of the image is delivered in form of an array. This method may be called repetitively later until the entire image data has been set.

• imageComplete: This method is called by the image producer once the whole image has been delivered to the image filter. Now that the whole image is known, the actual filtering can be performed. The resulting data has to be delivered to the image consumer that is placed after the image filter. This is done by calling the setPixel method of the following image consumer (this could be anything -- even another image filter). If we look back, this is the same way the data has been delivered to the image filter itself -- only this time it is the image producer.

Actually, there are two versions of the setPixel method:

void setPixels(int x, int y, int w, int h, ColorModel model, byte pixels[], int off, int scansize); void setPixels(int x, int y, int w, int h, ColorModel model, int pixels[], int off, int scansize);

The only difference is that one version delivers the image data in form of a byte array (e.g. grayscale or colormap images) and the other version in form of an integer array (e.g. in case of true color images). Every value of the array represents one pixel of the source image. The ColorModel object model encapsulates methods that should be used to translate the pixel values contained in the array into the alpha, red, green, and blue color components. This also means that different parts of the image can be delivered in different color models. In our case we want to find out the red, green and blue components of every pixel p, regardless how the pixel was stored in the source image. This is done by calling model.getRGB(pixels[p]).

So far, everything is set to take over the pixels from the source image. Still, there is another tricky part ahead. The array of pixels is usually larger then the (w, h)-sized rectangle. This is the reason for the additional arguments offset and scansizeof the setPixel method. The offset is the position of the pixel (x, y) in the array and scansize is the number of pixels that follow until the position (x, y+1) is reached. The pixel at a position at (x+i, y+j), with $(0 \le i < w)$ and $(0 \le j < h)$ located at index $offset + (j \cdot scansize + i)$ of the array.

Here is an example how the actual code looks like:

public void setPixels(int x, int y, int w, int h, ColorModel model, byte pixels[], int off, int scansize) { int srcoff = off; int dstoff = y * srcW + x; for (int yc = 0; yc < h; yc++) { for (int xc = 0; xc < w; xc++) { raster[dstoff++] = model.getRGB(pixels[srcoff++] & 0xff); } srcoff += (scansize - w); dstoff += (srcW - w); } }

The image producer calls the imageComplete method of the image filter once all pixels are handed over. This is the place where the actual filter algorithm is performed. All in the virtual laboratory used image filter are implemented as just explained. Figure 4.9 shows a summary of basic filter types, that have been derived from the jave.awt.ImageFilter class and sections 4.3.3.2 through 4.3.3.5 describe the particular filter types that have been developed.

  

Figure 4.9: Generic types of image filter derived from the Java ImageFilter class.

   
4.3.3.2 Geometric Transformations

A geometric transformation changes geometric properties of an image. For example rotating an image is a geometric transformation. Parts of the code that have to be created for the methods setPixel and imageComplete are almost identical for similar types of image filters. It is therefore a good idea to create an abstract image filter class for a group of similar image operation.

The abstract class TransformationFilter has been designed as a filter template that is used for geometrical image transformations. This class already implements the image consumer interface. A subclass has only to define how the pixels are actually transformed. This is done by overriding three methods:

public void transformBBox(Rectangle rect); abstract public void transform(double x, double y, double[] retcoord); abstract public void itransform(double x, double y, double[] retcoord);

The transform methods' task is to transform the coordinates of a pixel (x, y) of the source image into the coordinates it should get in the destination image. The itransform method has to perform the reverse transformation.

The method transformBBox has to calculate the boundaries of the resultant image after the geometric transformation. The TransformationFilter needs this information to determine the size and position of the image after transformation. The TransformationFilter class already contains a standard implementation of the transformBBox method, which can be used for some geometrical transformations. The standard implementation takes the coordinates of the four corner points and calculates the boundaries of the resultant image by transforming those corner points. This method, however, cannot be used to determine the boundaries for all transformations. It must be overridden for transformations that need to calculate the bounding box in a different way (see ClipFilter for example).

The TransformationFilter class generates the destination image by applying itransform to the coordinates of every pixel in the destination image. The pixel in the source image that is closest to the resulting position is taken and placed in the destination image (zero-order interpolation).

The following implemented filters are subclasses of the TransformationFilter:

  

Figure 4.10: Implemented transformation Filter

ClipFilter class

Constructor: public ClipFilter(Rectangle rect);

This simple operation cuts out an area of a given rectangle. The transform and itransform methods don't change the given coordinates. The pixels are just copied from the same position in the source image. The transformBBox method however returns the position of the desired area that wants to be cut out. The constructor argument rect specifies the area that is cut out.

MirrorFilter class

Constructor: public MirrorFilter(int dir, int width, int height);

This filter mirrors the whole image regarding the X or Y-axis. The standard transformBBox method is used. The mirror axis is defined by setting dir to MirrorFilter.HORIZONTAL or MirrorFilter.VERTICAL. The arguments width and height have to be the dimensions of the image.

ResizeFilter class

Constructor: public ResizeFilter(double zoomX, double zoomY);

The ResizeFilter class is used to scale an image. The transformation is performed by calculating: x_new= x_old * zoom_x and y_new = y_old * zoom_y. The boundary box is determined by the default implementation of transformBBox.

RotateFilter class

Constructor: public RotateFilter(double angle);

This filter generates an image that is rotated counterclockwise by angle degrees. The default implementation of transformBBox is again suitable for determining the bounding box. The transformation of each pixel is calculated according to:

$$\begin{align*}x_d &= \cos(angle) \cdot x_{src} - \sin(angle) \cdot y_{src} \\ y_d &= \cos(angle) \cdot y_{src} + \sin(angle) \cdot x_{src} \end{align*}$$

   
4.3.3.3 Spatial Filtering

Spatial filters perform a local operation for every pixel by using spatial masks. The center of this mask is moved across the image from pixel to pixel. Spatial filters can be divided into linear and non-linear filters. In case of a linear spatial filter, the basic operation is to calculate the sum products of the intensities of each pixels neighborhood and the mask coefficients of the spatial filter. Examples of linear filters are lowpass and highpass mask filters, which suppress certain frequency components in the Fourier domain.

Non-linear spatial filters also operate on a neighborhood of a pixel. They are not specified by mask coefficients however. For example, the median filter is an example of a non-linear spatial filter.

A special class named MaskFilter has been implemented as a super class for all spatial filters (see figure 4.11).

  

Figure 4.11: Several implemented mask filters, derived form the MaskFilter class.

The constructor of the MaskFilter class takes two arguments that define the size and the mode that the filter should have. The mode designates the color channels that should be manipulated by the filter. The desired channels are defined by setting the necessary bits of mode using the following constants.

MaskFilter.CHANNEL_RED = 1	Red components are filtered
MaskFilter.CHANNEL_GREEN = 2	Green components are filtered
MaskFilter.CHANNEL_BLUE = 4	Blue components are filtered
MaskFilter.GRAY_MODE = 100	Each pixel is converted into grayscale before it is filtered.

For example, a value of 5 would cause a filtering of the red and green components of the image. The GRAY_MODE bit overrides the channel bits and indicates that the image has to be converted into gray scale before it is filtered.

The abstract method calculateChannel has to be implemented by every subclass. The filter operation has to be performed here. This method is called for every selected color component of every pixel. The intensities of the pixel and its neighborhood are delivered by the array area. It is a two-dimensional array of the size (n, n). The size n of the neighborhood is defined by the class constructor. The neighborhood of corner pixels that reach over the defined image area is determined by mirroring the image on its edges.

The following classes are spatial filters that implement the MaskFilter class:

LowPassFilter class

Constructor: public LowPassFilter(int n);

A lowpass filter is a linear filter that reduces the low frequency components of the image. Sudden changes in the intensities of neighboring pixels are smoothed out. This may have a blurring effect on the image depending on the size of the mask. Such filters may, as an example, be used as a cosmetic process to reduce noise or to smooth images digitized with a low number of gray levels.

The LowPassFilter class implements a simple lowpass filter that uses a (n, n)-sized rectangular mask in which all coefficients are set to 1.

$$M=\frac{1}{n^2} \begin{bmatrix} 1 & 1 & \cdots & 1 \\ 1 & 1... ...vdots & & \ddots & \vdots \\ 1 & 1 & \cdots & 1 \end{bmatrix}$$

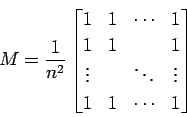
The filter operation is simply an averaging of the pixels in the area over the mask.

MedianFilter class

Constructor: public MedianFilter(int n);

The median filter is a non-linear approach to reduce noise. The median filter is especially suited to reduce spike like noise. A pixel is hereby replaced by the median of the gray values of its neighborhood. The median of a (n, n)-sized area, with n an odd number, is defined as the ((n*n)+1)/2 largest gray value of this area. For example, the median of a 3 by 3 neighborhood is obtained by choosing the fifth largest value of that area. The MedianFilter class uses an implementation of the median algorithm explained in [2], which calculates the median in O(n) time.

HighPassFilter class

Constructor: public HighPassFilter(int n);

The HighPassFilter class utilizes a highpass spatial filter. Highpass filters use masks with a positive coefficient near its center surrounded by negative coefficients. This class uses a mask with all coefficients except the center coefficient set to -1. The center however is the absolute value of the sum of all other coefficients. The overall sum of all coefficients always equal to zero. Following is an example of a 3 by 3 mask.

$$M=\frac{1}{9}% \begin{bmatrix} -1 & -1 & -1 \\ -1 & 8 & -1 \\ -1 & -1 & -1 \end{bmatrix}$$

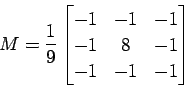
The size n must again be an odd number and is set with the constructor. Moving the mask over an area with almost the same gray levels is producing zero or very low values. The higher the difference of gray levels of neighboring pixels the higher is the magnitude of the output. Thus, this filter is enhancing the edges (high frequency components) of the image. Negative results of the mask operation are clipped to zero.

HighBoostFilter class

Constructor: public HighBoostFilter(int n, float bfactor);

The highpass filter has the disadvantage that it eliminates the zero-frequency term. This is noticeable at the reduced contrast of the resultant image. Better results are obtained by high boost filters. Those filters overlay the original image with a highpass filtered version of the image. The edges of the image are again enhanced but parts of the low frequency components are also kept. The filtered image looks more like the original image. The filter mask is almost identical to the one of the highpass filter although the center coefficient is replaced by n²*bfacter-1. The boost factor (bfactor) determines to what extent the result is influenced by the original image. This factor should be larger then 1. A value of one produces results similar to the plain highpass filter.

SharpenFilter class

Constructor: public SharpenFilter(int type, int tresh, int lb, int lg);

This filter emphasizes the edges of an image by calculating the gray level gradient of every pixel. Actually, only an approximation of the magnitude of the pixels gradient is computed by using the sum of two Roberts cross-gradient operators [4].

Additionally, one of five thresholding operations can be performed. This is specified by using one of the constants shown in table 4.1 for the constructor argument type.

 

Table 4.1: Different possible constants, that should be used for the constructor argument type to set the sharpen type of the SharpenFilter object.

Type	Result
SharpenFilter.METHODE1	No thresholding is performed. The values in the resultant image are replaced by the gradients of the original image.
SharpenFilter.METHODE2	Only pixels whose gradient is greater or equal trash are replaced by the gradient. All other pixels stay unchanged.
SharpenFilter.METHODE3	Pixels whose gradient is greater or equal trash are replaced by the gray value lg.
SharpenFilter.METHODE4	Pixels whose gradient is greater or equal trash are replaced by their gradient. All other pixels are set to gray value lb.
SharpenFilter.METHODE5	Pixels whose gradient is greater or equal trash are replaced by gray value lg. All other pixels are set to gray value lb.

 

   
4.3.3.4 Point Processing

There is another group of image enhancement methods, which only process the intensities of single pixels. They do not change the location of a pixel nor need information about its neighborhood. An equal sized image is produced whose resultant pixels depend only on the corresponding pixels in the source image. The AWT already provides a class named RGBImageFilter that is suitable for such filters. Those filters are easy to create since the RGBImageFilter already implements the setPixel and imageComplete methods. However, a new method named filterRGB must be overridden:

public int filterRGB(int x, int y, int rgb);

The value rgb represents the color information of a pixel at position (x, y). The filterRGB method has to calculate the new color of that pixel. The following filters have been implemented that way:

  

Figure 4.12: Implemented point processing filter.

BlackWhiteFilter class

Constructor: public BlackWhiteFilter(int thresh);

This filter generates a black and white version of the source image. A pixel is set to black if its gray value is below tresh. Non-gray scale pixels are converted into grayscale before the threshold is applied.

SaturationFilter class

Constructor: public SaturationFilter(double sat);

The saturation filter can be used to change the overall saturation of an image. The red, green and blue values of each pixel are converted into the HSV model. This is done by using the method RGBtoHSB of the java.awt.Color class. The saturation is multiplied by sat which is set with the constructor. The resulting saturation value is clipped to one if it exceeds one. This filter can also be used to convert a color image into gray scale by setting sat to zero.

   
4.3.3.5 Histogram Operations

Given a grayscale image, the histogram is a discrete function p(r_k) that computes the number of pixels for each gray level of that image.

p(r_k)=n_k

Where r_k is the kth intensity level and n_k is the number of pixels with that intensity. Three separate histograms can be generated for each color channel of a color image. Since the AWT images are using 8 bit for each color channel, k is in the range of 0 to 255.

A class named Histogram (figure 4.13) has been created that calculates and encapsulates the histogram of an image. Other components of the system use this class to display or manipulate the histogram.

  

Figure 4.13: The Histogram class.

The constructor takes only one argument, which is an instance of the GipImage class. Calling the generate method computes the histograms for the intensity levels of the channels red, green and blue. Internally the pixels are extracted with the help of the java.awt.PixelGrabber class. The results are stored in the arrays red, green and blue of the Histogram object.

Histogram equalization and histogram specification are two image-processing methods that both use the histogram information encapsulated in the Histogram object. These two operations are again implemented as subclasses of the AWT ImageFilter.

HistEqualFilter class

Constructor: public HistEqualFilter(Histogram histogram, Point size, int color);

The goal of histogram equalization is to map the intensity levels of pixels so that the resultant image has equal numbers of pixels for each intensity level. This implies that the histogram of the resultant image contains only equal values.

A mapping function v=T(s) is sought that maps the original intensity levels s into new levels v. Let's consider first, that the histogram function is continuos. According to [4], the mapping function T(s) can be calculated by building the integral over the histogram function p(r) that way:

$$T(s)=\int_{0}^{s}\frac{p_r(j)}{n}\,dj$$

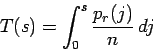
Since the histogram consists of discrete values, a discrete form of this integral must be used:

$$T(s)=\sum_{j=0}^{s}\frac{p_r(j)}{n}$$

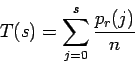
The HistEqualFilter filter exactly implements this function. The constructor takes three arguments: histogram, size and color. The argument histogram has to be an instance of the Histogram class, which contains the histogram of the image that should be processed. The argument size defines the dimensions of that image and color specifies the color channels that should be processed. The following table shows the class constants that should be used to define color:

HistEqualFilter.CHANNEL_RED = 1; HistEqualFilter.CHANNEL_GREEN = 2; HistEqualFilter.CHANNEL_BLUE = 4;

For example setting color to (HistEqualFilter.CHANNEL_RED + HistEqualFilter.CHANNEL_GREEN) would cause the processing of only the red and green components of the image.

HistSpecFilter class

Constructor: public HistSpecFilter(Histogram histogram, int[] z, Point size, int color);

The histogram equalization as explained above is actually only a special case of a whole group of histogram operations called histogram specification [4]. Histogram specification is used to shape the original histogram p_r(r) so that the resultant image obeys a desired histogram p_z(z).

In order to explain how this is done, we start by equalizing the original histogram again:

s = T_r(r)

Of course equalizing the desired histogram p_z(z) is also possible:

v = T_z(z)

Since histogram equalization always produces the same uniform histogram, we can set: p_s(s) = p_v(v). The inverse function z = T_z^-1(v) can now be used to calculate the desired histogram p_z(z):

z = T_z^-1[T_r(r)]

The HistSpecFilter uses this principle to generate a table, which maps the intensity levels of the original image into new intensity levels. The calculation is done in three steps:

1.

Two arrays T_r[] and T_z[] are generated that represent the mapping functions T_r(r) and T_z(z). For example, T_r[i] is set to the equalized intensity level of the corresponding level i in the original image.

2.

A third array G_z[] is generated, which contains the inversion of T_z[]. For example, if T_z[4] = 17 then G_z[17] = 4.

3.

G_z[] and T_r[] can now be used to determine the resulting intensity levels: z = G_z[T_r[r]]

This is however only correct if T_z^-1[v] is single-valued, which is generally not the case. G_z[] can contain ''holes'' that would produce undefined mappings. This is prevented by setting the blank fields to the lowest defined neighbor value. For example, if G_z[17] = 4, and G_z[18] and G_z[19] are undefined, then those two fields are also set to 4.

The constructor of the HistSpecFilter class takes the same arguments as the HistEqualFilter. Additionally, the desired histogram is specified by the array z.

4.3.4 Serialization of AWT images in Java 1.1.x

One problem that occurred during the development of the GipImage class was that Java's java.awt.Image class does not implement the Serializable interface. This means that an instance of the java.awt.Image class cannot be serialized. Nevertheless, serialization is needed to transport objects for RMI calls. That makes the AWT Image object unusable for RMI; a problem that many programmers have experienced as was noticeable on frequently asked questions in Java forums and newsgroups. The following paragraphs explain a workaround for that problem.

During the serialization, the GipImage and possible member variables, except the AWT image, are serialized successfully. However, the serialization process fails once it's the image's turn to be exported. The AWT image must be converted into a serializable form before the serialization can take place. This has been done by extracting the pixels of the image and putting those values into an array. The array can now be serialized since all primitive Java variables are serializable.

Since there is actually no direct way to access the pixels of an AWT image, pixels must be accessed through an implementation of the ImageProducer and ImageConsumer interface. AWT provides a class named PixelGrabber, which is an ImageConsumer that performs this task. An instance of the PixelGrabber class is attached to an image, which retrieves the pixels of that image into the array.

The AWT image variable itself has to be declared transient. The serialization process ignores transient variables. Now, the serialization of a GipImage object is not producing an error during serialization anymore. Everything that is required to reconstruct an instance of the class, including the following is automatically exported during serialization:

• Class of the object
• Class signature
• Values of all non-transient and non-static members, including members that refer to other objects

That means if we make our array a class member variable, it is also automatically serialized. However, the AWT image object itself is not be serialized since we declared it transient. Finally, the AWT image can be reconstructed at the receiver by using AWT's MemoryImageSource class, which is an implementation of the ImageProducer interface.

  

Figure 4.14: A schematic diagram that shows how objects are transmitted as serialized stream.

The question still remains about when the image is converted to and from the array. The serialization can be customized by providing two methods named writeObject and readObject, which are both defined by the Serializable Interface. Those methods are called before and after serialized objects are exported and imported. It is sufficient to convert the image into an array within the writeObject method. To enhance transmission speeds, the array is compressed with the help of the java.util.zip.Inflater class. Later, it is decompressed and converted back again in the readObject method.