4.4 Drawings (class GipDrawing)

Drawings are 2D objects that are displayed on top of an image. A class named GipDrawing as shown in figure 4.15 has been designed as a prototype for all types of drawing. All implemented drawings have are common in that they are defined by a set of control points. For example, the control points of a circle are the center of the circle and a point on its perimeter. The class GipDrawing uses a Jawa.util.Vector to store those control points (variable pointList). It also includes methods that deal with the creation and the manipulation of the drawing.

  

Figure 4.15: The GipDrawing class.

Definition of control points:
The GipDrawing works very close together with the image window, since the image window provides the mouse event routines that are needed to create a drawing. An instance of the GipDrawing class is generated when the user selects a drawing from the menu system of the image window. Following class constructor is provided by the GipDrawing class:

Constructor: public GipDrawing(int id, int parentId, int user, int min, int max, Color c, int lw);

The parentId is the ID of the image that is associated with this drawing. The arguments min and max declare the minimum and maximum number of control points that this drawing can have. Constructors of subclasses must call this constructor with appropriate values. For example, a circle has a min and max value of two. Further, the arguments c and lw define the color and line width in which the 2D object is drawn.

A newly instantiated drawing object is first in creation mode, where it is painted in XOR mode. The drawing can be moved and changed faster, since the whole image doesn't need to be redrawn after every change. The drawing can easily be deleted and repainted that way.

Since there are no control points defined yet, there is also nothing drawn at first. Every time the user clicks on the image canvas, the method addPoint is called. This adds the coordinates of a control point to the drawing. The user can change this control point while the mouse button is held down. The method changePoint is called every time the cursor is moved with pressed mouse button. The paint method, which paints the drawing onto the image canvas, is called once before and once after changePoint is called. Since the drawing is painted in XOR-mode, the old drawing is erased and repainted with the changed control point that way. This process is repeated until the maximum number of control points is reached or the right mouse button event is received. This causes the image window to call the drawings's finish method, which sets the drawing into solid mode.

  

Figure 4.16: Event sequence, when creating a drawing.

The drawing is from now on painted in a solid shape with defined color and line width. The AWT calls the paint method of the image window every time the image needs to be repainted. This method has been overridden and changed so that it is calling the paint method of all GipDrawing objects that are associated with the image.

Moving a drawing:
The user can select and move a drawing by clicking on it. When the image window receives a mousePressed event, it calls the distance method for all its drawing objects. This method calculates the shortest path between the drawing and the coordinates of the mouse click. The standard implementation of the GipDrawing class simply returns the distance to the control point that is closest to the clicked point. Subclasses that need to calculate the distance in a different way override this method.

The image window selects the nearest drawing object and calls the method editMode(true). This sets the drawing into edit mode, which actually causes the drawing to be painted in xor mode again. The image window is now calling the move method for every received mouseDragged event. The move method dislocates the drawings control points by the distance provided by the mouseDragged event. The drawing is then removed and repainted from the image canvas.

The drawing stays in xor mode unless a different drawing is selected. In that case the drawing is set back into solid mode by calling editMode(false).

Manipulation of drawings:
In addition to the control points, every drawing subclass can have its own set of properties. The drawing object creates a dialog window on demand that lets the user change those attributes. The image window calls the editProperties method if it receives a double click event. It determines the appropriate object again by using the distance method.

Geometric transformation of drawings:
A geometric transformation that is performed on an image needs to be performed for all its drawings also. Transformations are implemented as Java Image Filters (class TransformationFilter) as explained in section 4.3.3.2. The GipDrawing class contains a method named transform, which takes an instance of the TransformationFilter class as argument. This method itself uses the transform method of the filter in order to transform the coordinates of all control points. The drawing is repainted once the new coordinates of all control points are known.

4.4.1 Implemented Types of Drawing Objects

Several types of drawings, based on the abstract class GipDrawing, have been implemented (shown in figure 4.17). As a minimum, a subclass must override the paint method. This method uses the list of control points to paint the drawing on the image canvas. Usually, a subclass overrides the methods distance and editProperties also. Figure 4.17 shows the inheritance tree of all implemented drawing classes.

The class GipArrowDrawing is an abstract class that contains a method named drawArrow. All drawing objects that have straight endings are inherited from this class. They use the drawArrow method in case the drawing should have arrows at the ends. The method takes as argument two points, which represent an end-segment of the drawing. The method determines the angle of the line and paints two additional short lines 30 degree apart from the tip of the line.

The following table shows a summary of all implemented objects together with their minimal and maximal number of control points and a description of the objects shape.

Class	min. points	max. points	Shape
GipPolyLine	2	$\infty$	Connects the control points in the given order with straight lines.
GipLine	2	2	A straight line. This is a subclass of GipPolyLine that simply sets the min. number of control points to 2.
GipSpline	3	$\infty$	A 3rd degree curve that is interpolated through the set of control points (see section 4.4.2).
GipBezier	3	$\infty$	A 3rd degree curve that is approximated through the set of control points (see section 4.4.3). The curve meets however the first and the last control point.
GipBox	2	2	The two control points define the upper left and lower right coordinates of the box.
GipFilledBox	2	2	The same as GipBox class. It paints only a filled circle.
GipCircle	2	2	The first control point declares the center of the circle. The second control point defines a point on the perimeter of the circle, which actually defines the radius to the center.
GipFilledCircle	2	2	A filled version of the GipCircle class.
GipEllipse	2	2	The first control point defines the center of the ellipse. The horizontal and vertical distance of the second control point define the two radii of the ellipse. The axes of the ellipse are always parallel to the coordinate system.

  

Figure 4.17: An summary of all implemented drawing classes.

   
4.4.2 Interpolated Cubic Curves

The class GipSpline implements a cubic curve that is passed through the set of given control points. The curve itself is divided into curve segments. The control points are the ends of each segment. Two segments are joined at a common control point.

Each curve segment can be defined in parametric form: $Q(t) = [x(t)\ y(t)]$, where the parameter t is restricted to a [0, 1] interval. x(t)and y(t) are cubic polynomials of the form:

$$\begin{align*}x(t) &= a_x t^3 + b_x t^2 + c_x t + d_x \\ y(t) &= a_y t^3 + b_y t^2 + c_y t + d_y \end{align*}$$

This equation can also be expressed in following matrix form:

$$Q(t)=T \cdot C \qquad \text{with}\ T = [t^3\ t^2\ t\ 1]$$

Where C is the matrix of coefficients of the two polynomials.

The coefficients of the cubic equation can be calculated by knowing at least four boundary conditions. Those conditions define the nature of the curve. Usually they are the coordinates of the curve segments of the points at t = 0 and t = 1 (which are the control points) together with their derivative (the tangent vectors at the control points). Such curves are called Hermite Curves. In our case, the curve should only be interpolated through a given series of control points. The tangent vectors of the control points are not known. A member of the Catmull-Rom family ^4.2 has been used in this case [3]. Here, the tangent vector at a point p_i is set to the vector represented by the line connection between p_i-1, p_i+1. The boundary conditions of the curve segment at t=0and t=1 are now defined:

$$\begin{align*}Q(0) & = p_k \\ Q(1) & = p_k + 1 \\ Q'(0) & = \frac{1}{2}(1-tens... ...p_{k+1}-p_{k-1}) \\ Q'(1) & = \frac{1}{2}(1-tension)(p_{k+2}-p_k) \end{align*}$$

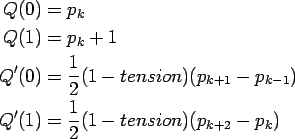
The parameter tension controls how loosely or tightly the spline fits the control points. The higher the tension parameter the tighter are the curves at the control points.

The curve equation can now be solved with the help of the control point conditions which, in turn, leads to the following solution [5]:

$$Q_k(t) = [t^3\ t^2\ t\ 1] \cdot M \cdot G_k = [t^3\ t^2\ t\ 1... ...} p_{k-1} & \\ p_k & \\ p_{k+1} & \\ p_{k+2} & \end{bmatrix}$$

The equation has been simplified by substituting $s = \frac{1}{2}(1-tension)$. The matrix M and the vector G_k are called basis matrix and geometry vector. G_k defines the geometric constraints of a curve segments. Expanding this equation, we get the following form:

$$Q_k(t) = p_{k-1} \cdot C_0(t) + p_k \cdot C_1(t) + p_{k+1} \cdot C_2(t) + p_{k+2} \cdot C_3(t)$$

The terms C_k(t) for k=0, 1, 2, 3 are called blending functions, which are:

$$\begin{align*}C_0(t) & = -2 \cdot t^3 + 2s \cdot t^2 - s \cdot t \\ C_1(t) & = ... ...-2s) \cdot t^2 + s \cdot t \\ C_3(t) & = s \cdot t^3 - s \cdot t^2 \end{align*}$$

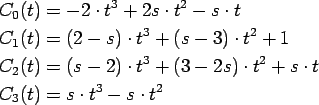
Given n control points p₀, $\ldots$, p_n-1, each of the n-1 curve segments can be drawn by using the function above. However, the tangent vectors of the first and the last segment are not defined yet. This can be fixed by introducing two additional points p_-1 and p_n, which are set to the first and the last control point:

$$\begin{align*}p_{-1} & = p_1 \\ p_n & = p_{n-1} \end{align*}$$

This means that the tangent vector of the first control point is set to the direction of the line connection p₁, p₂. This is done similar for the last control point as well.

   
4.4.3 Approximated Cubic Curves

The class GipBezier represents curves similar to the GipSpline class. The curve should this time however be approximated instead of interpolated. An implementation of a cubic uniform nonrational B-Spline according to [3] has been used. The B-Spline approximates a series of n control points. The curve is again divided into n-1 curve segments. Consecutive segments have common join points, which are called knots. A segment i is defined by four control points: p_i-3, p_i-2, p_i-1 and p_i. Those points again build a geometry vector G:

$$G = % \begin{bmatrix} p_{i-3} \\ p_{i-2} \\ p_{i-1} \\ p_i \end{bmatrix}$$

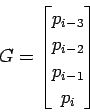
The geometric constraints G, together with the basis matrix M for B-Splines (gathered from [3]), are again used to calculate the curve segment:

$$M = \frac{1}{6} \cdot % \begin{bmatrix} -1 & 3 & -3 & 1 \\ 3 & -6 & 3 & 0 \\ -3 & 0 & 3 & 0 \\ 1 & 4 & 1 & 0 \end{bmatrix}$$

$$\begin{split} Q(t) &= T \cdot M \cdot G_k \\ &= \frac{(1-t)... ...3t^3 + 3t^2 + 3t + 1}{6}p_{i-1} + \frac{t^3}{6}p_i \end{split}$$

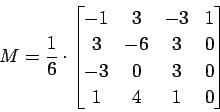
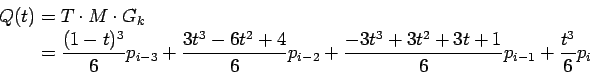
The B-Spline should additionally be forced to meet the first and the last control point. We can use the fact, that a curve can be pulled closer to a control point by replicating the concerning control point. The curve completely meets a control point if this point is used at least three times. Exactly this is done for the first and the last control point as follows:

This actually introduces two additional curve segments. The complete curve is now drawn in n+1 steps. The first segment starts at point p₀and the (n+1)th segment ends at the last control point p_n-1.